This is the page
27 Gennaio 2019
è arrivato … il Cantastoria
27 Gennaio 2019di Luigi Pellegrini
4. Altre costruzioni più complesse
Esercizio 4.1:
Data una circonferenza e un punto P fuori di essa determinare le tangenti ad essa passanti per P.
Trovare il punto medio M tra il centro O della circonferenza e il punto P. Trovare la circonferenza di centro M passante per P. I punti di intersezione delle 2 circonferenze sono i punti in cui le rette per P sono tangenti alla circonferenza data.
E’ utile costruire la macro che ha come oggetti iniziali la circonferenza di centro O e il punto P e come punti finali le due rette tangenti.
Esercizio 4.2:
Date due circonferenze determinare le 4 rette tangenti a entrambe le circonferenze.
Per questa costruzione ho utilizzato un metodo non puramente geometrico che, sebbene non molto elegante, si è rivelato utile in più di una occasione. Esso si basa sull’utilizzo dello strumento calcolatrice.
Una retta tangente a entrambe le circonferenze forma con la congiungente i due centri 2 triangoli rettangoli simili: le distanze OP = R, O’Q = r e OO’ = d sono date, chiamiamo x la distanza AO, risulta quindi
AO’ = d – x , per cui si può impostare la proporzione
x : R = (d – x) : r
Risolvendo si ottiene
Procedimento:
con lo strumento misura di lunghezza misurare i due raggi R e r delle due circonferenze e la distanza d = OO’.
strumento calcolatrice: trascinare le misure d, r e R dentro la finestra di calcolo e calcolare x secondo la formula precedente; trascinare il risultato nell’area di disegno. Questo valore, essendo dipendente da d, r e R, cambierà modificando la figura.
strumento semiretta: disegnare la semiretta di origine O passante per O’
strumento trasporto di misura: trasportare la misura trovata x sulla semiretta OO’, si trova così il punto A.
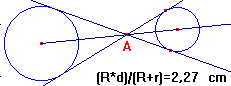
Usando ora la macro costruita nell’esercizio 4.1 si trovano le rette tangenti alle circonferenze passanti per A.
Ragionando e operando analogamente si trovano le altre 2 rette tangenti:
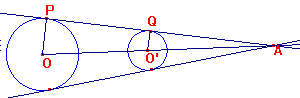
Esercizio 4.3: (problema semplificato dei cerchi di Apollonio)
Date tre circonferenze di uguale raggio, determinare due circonferenze che sono tangenti a tutte e tre le circonferenze date.
Bisogna anzitutto costruire 3 circonferenze di uguale raggio. Per questo si può adoperare 3 volte lo strumento “compasso“: disegnare un segmento AB e poi con il compasso disegnare 3 circonferenze di raggio AB e centri O, P e Q.
Una circonferenza tangente esternamente alle 3 circonferenze avrà il centro equidistante dalle 3 circonferenze e dunque equidistante da O, P e Q, coinciderà quindi con il circocentro del triangolo OPQ. I punti di tangenza saranno ovviamente sulla congiungente il circocentro con i punti O, P e Q.
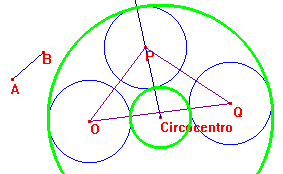
Disegnare dunque le circonferenze aventi per centro il circocentro e passanti per uno di questi punti.
di Luigi Pellegrini
2. Le macro
Le macro in cabri-géomètre servono per produrre nuovi strumenti. Sono molto utili quando si eseguono lavori complessi o consistenti di tante “parti elementari”.
La casella “macro” consiste di 3 strumenti:
che significa “oggetti iniziali”
che significa “oggetti finali”
che significa “definizione della macro”
Per capirne il funzionamento consideriamo il seguente esercizio:
Esercizio 2.1:
Costruire la macro “circocentro” di un triangolo.
Utilizziamo l’ex. 1.4 (circocentro di un triangolo).
Premere il pulsante 
, selezionare il triangolo.
Premere il pulsante 
, selezionare il circocentro
Premere il pulsante 
e compilare la finestra che appare nel seguente modo:
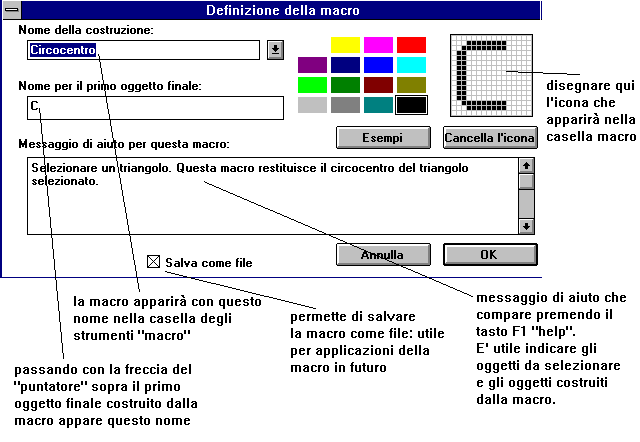
Questo aggiunge una icona nella casella degli strumenti macro. Selezionando un qualunque triangolo questa macro costruisce il circocentro del triangolo dato.
Si può fare lo stesso esercizio costruendo anche le macro “baricentro di un triangolo” e “circocentro di un triangolo”.
E’ bene salvare le macro costruite “come file”, in modo che queste possano essere riutilizzate in futuro (una macro non salvata va persa chiudendo Cabri-géomètre)
