
This is the page
27 Gennaio 2019
è arrivato … il Cantastoria
27 Gennaio 2019di Luigi Pellegrini
6. Luoghi geometrici
Il luogo geometrico è uno strumento della casella costruisci. Il luogo geometrico è generato da un punto, che a sua volta dipende da un punto vincolato su una retta o semiretta.
Per costruire un luogo si indica l’oggetto che lo genera e successivamente il punto vincolato su una retta o semiretta.
Esercizio 6.1:
La bisettrice come luogo geometrico.
Aprire il file dell’esercizio 5.1. Selezionare lo strumento luogo, poi il punto P (che, per come è stato costruito è equidistante dai lati dell’angolo e quindi genera il luogo) e il punto A (vincolato sulla semiretta). Viene costruita la bisettrice, luogo dei punti equidistanti dai lati dell’angolo.
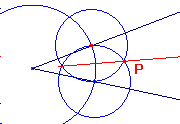
Cabri-géomètre costruisce un luogo per punti; per aumentare la precisione del luogo occorre quindi agire sul numero di punti che danno origine al luogo. Per default essi sono 50. E’ possibile cambiare questo valore andando nel menu opzioni, preferenze, opzioni per i luoghi.
Esercizio 6.2:
L’asse come luogo geometrico.
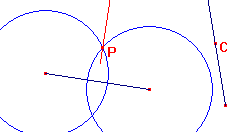
Aprire il file dell’esercizio 5.2. Selezionare il punto P (equidistante dagli estremi del segmento) e poi il punto C (vincolato sulla semiretta). Viene costruita l’asse del segmento.
Esercizio 6.3:
Srotolare una circonferenza.
Immaginiamo un cilindro con avvolto un filo. Se leghiamo alla punta del filo una matita, quale sarà il luogo descritto dalla matita nello srotolare il filo?
Visualizzare gli assi cartesiani con lo strumento “mostra gli assi“. Costruire quindi la circonferenza di centro l’origine e raggio 1. Con lo strumento “arco di circonferenza” della casella curve costruire due semicirconferenze (passanti per i punti (1,0), (0,1) e (-1,0) la prima, (-1,0), (0,-1) e (1,0) la seconda).
Facciamo questo perché Cabri-géomètre fa confusione con gli angoli maggiori di pi greco.
Nascondere ora con lo strumento “mostra/nascondi” la circonferenza iniziale e posizionare un punto P sulla semicirconferenza nord e un punto Q sulla semicirconferenza sud.
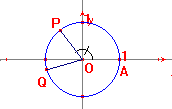
Segnare ora gli angoli AOP e BOQ e misurarli. Trovare ora le semirette tangenti in P e Q alle due semicirconferenze e trasportare (strumento trasporto di misura) su quella nord la misura dell’angolo AOP – punto M – e su quella sud la misura (AOQ+3,14), quest’ultima trovata mediante la calcolatrice – punto N.
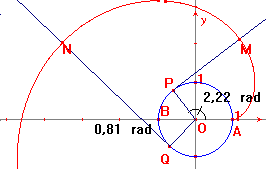
Il luogo generato da M quando P varia sulla semicirconferenza nord e quello generato da N quando Q varia sulla semicirconferenza sud costituiscono il luogo cercato.
Esercizio 6.4:
La spirale di Archimede.
La spirale di Archimede è il luogo dei punti definito dall’equazione in coordinate polari
r=t
dove
r = raggio
t = angolo
Come per l’esercizio 6.3 disegnare una circonferenza unitaria e le due semicirconferenze nord e sud sulle quali segneremo i punti P e Q, e misurare gli angoli AOP e BOQ.
Trasportare AOP sulla semiretta OP, trovando il punto M.
Trasportare BOP sulla semiretta OQ, trovando il punto N.
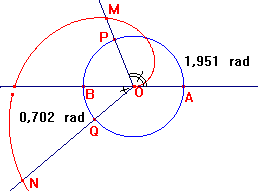
Il luogo generato dai punti M e N al variare rispettivamente di P e Q sulle semicirconferenze è la spirale di Archimede cercata.
Esercizio 6.5:
r=cos(2t).
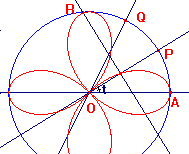
Costruire la circonferenza unitaria di centro O e selezionare un punto P su di essa. Costruire il simmetrico Q di A rispetto alla retta OP e poi il simmetrico R di P rispetto alla retta OQ.
Il piede della perpendicolare ad OP passante per R è un punto tale che la sua distanza da O eguaglia il coseno dell’angolo AOP, e quindi genera il luogo al variare di P sulla circonferenza.
Esercizio 6.6:
La lumaca di Pascal (luogo dei piedi delle perpendicolari condotte da un punto dato A alle tangenti a una circonferenza data).
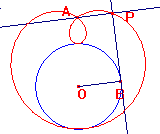
Data la circonferenza di centro O e il punto A fuori di essa, segnare un punto B sulla circonferenza e trovare la tangente in B alla circonferenza.
Il punto di intersezione tra la perpendicolare a detta tangente passante per A e la tangente stessa determina il punto che genera il luogo al variare di B sulla circonferenza.
