
This is the page
27 Gennaio 2019
è arrivato … il Cantastoria
27 Gennaio 2019di Luigi Pellegrini
7. Le coniche come luoghi geometrici
L’esempio più classico di luoghi geometrici sono senz’altro le coniche. Cabri-géomètre ha uno strumento che costruisce una conica passante per 5 punti, ma può essere istruttivo costruire le coniche secondo la definizione classica.
Esercizio 7.1: (parabola)
Costruire il luogo dei punti equidistanti da una retta (direttrice) e da un punto (fuoco).
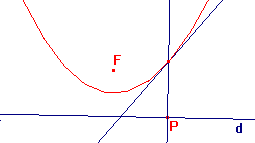
Assegnata la retta d e il punto F, costruiamo il punto P su d, quindi l’asse del segmento FP e la perpendicolare a d passante per P.
Il punto d’incontro tra le due rette or ora costruite genera una parabola di fuoco F e direttrice d, al variare di P sulla retta d.
Per verificare che effettivamente si tratta di una parabola, con lo strumento conica della casella curve costruiamo la conica i cui 5 punti stanno sul luogo testè costruito. Essi coincidono.
Esercizio 7.2: (ellisse)
Costruire il luogo dei punti la cui somma delle distanze da 2 punti dati (fuochi) è costante.

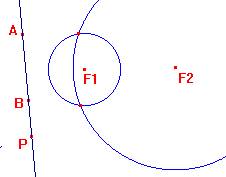
Dati i due punti F1 e F2 (fuochi) e il segmento AB (somma costante delle distanze) costruire un punto P su AB e i due segmenti AP e PB.
Con lo strumento compasso costruire le circonferenze di centro F1 e raggio AP e di centro F2 e raggio PB.
Il luogo generato dai punti di intersezione delle 2 circonferenze al variare di P sul segmento è l’ellisse cercata.
Come per la parabola costruire la conica avente 5 punti sul luogo appena costruito.
Esercizio 7.3: (iperbole)
Costruire il luogo dei punti la cui differenza delle distanze da 2 punti dati (fuochi) è costante.

Assegnati due fuochi F1 e F2, sia AB il segmento differenza (costante) delle distanze dai fuochi.
Un punto appartenente a tale iperbole sarà allora il punto dintersezione tra le circonferenze di raggio AP (di centro F2) e BP (di centro F1) – usare lo strumento compasso con i segmenti AP e BP.
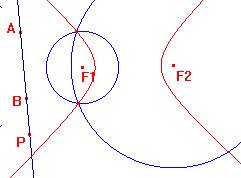
Il luogo generato da Q e R al variare di P sulla retta costruisce l’iperbole cercata (per visualizzare meglio l’iperbole usare lo strumento conica e selezionare 5 punti sul luogo appena costruito.
Esercizio 7.4:
Costruire il luogo dei punti equidistanti da una circonferenza di centro F2 e da un punto F1 interno alla circonferenza stessa.
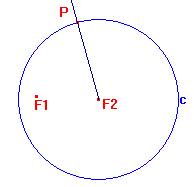
Sia c la circonferenza in questione.
Semiretta di centro F2 con un punto P su c.
Un punto equidistante dalla circonferenza in P e da F1 sarà il punto dintersezione Q tra la semiretta e lasse del segmento PF1:
Asse di PF1:

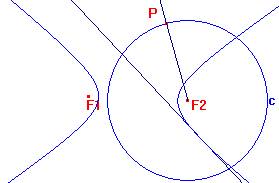
Il luogo generato da Q al variare di P su c è quel che stavamo cercando (anche qui selezionare con lo strumento conica 5 punti su tale luogo).
Spostando F1 fuori da c otteniamo uniperbole.
