CORSO DI CABRI GEOMETRE

di Luigi Pellegrini

12. Uso di Derive

1. Creare e semplificare espressioni

Menu semplifica

·  Semplificare espressioni

   

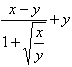
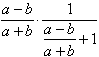
La seconda espressione non viene semplificata: questo perché non si è specificato il dominio di definizione delle variabili (). Questo si può fare attraverso il menu dichiara > dominio di una variabile. Ogniqualvolta Derive non fa quel che ci si aspetta è utile controllare che i domini delle variabili coinvolte siano corretti.

·  Sviluppare espressioni

   

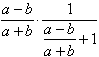
·  Fattorizzare espressioni

;  ; 

·  Approssimare espressioni (col numero di cifre voluto)

 

Osservazione:

Con le approssimazioni bisogna stare attenti. Vediamo un esempio:

Calcolare l’espressione:

in x=1 000 000

Si ottiene 0: il motivo è che per default derive usa 10 cifre significative per svolgere i calcoli approssimati. Si può variare questo valore con dichiara > impostazioni di semplificazione.

2. Ricerca degli zeri di un polinomio

Dato il polinomio y=p(x) vogliamo trovare gli zeri di p(x).

Possiamo seguire innanzitutto un approccio grafico: dopo aver inserito il polinomio nella finestra algebra, passare alla finestra grafica 2D e disegnare p(x). Il pulsante modalità traccia posiziona il cursore sulla curva, che può essere spostato con i tasti direzione. Usando in modo appropriato i pulsanti di ingrandimento si possono trovare gli zeri di p(x) con l’approssimazione voluta.

Oppure si può usare la funzione SOLVE (oppure il menu risolvi > espressione) per risolvere lequazione associata. Notare che se il polinomio è di grado >=5 e non è scomponibile derive troverà degli zeri approssimati.

La funzione SOLVE restituisce la soluzione nella forma .

3. Equazioni e disequazioni

Come abbiamo appena visto la funzione SOLVE permette di risolvere equazioni e disequazioni. Il menu risolvi > sistema (che utilizza ancora la funzione SOLVE) consente inoltre di risolvere sistemi di equazioni e disequazioni.

Esempi:

   

   

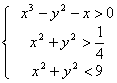
In alternativa possiamo usare la funzione SOLUTIONS, utile nel caso dovessimo rappresentare le soluzioni come punti, che restituisce un vettore di vettori (matrice) di soluzioni dellequazione o del sistema di equazioni.

E utile rappresentare nella finestra grafica le soluzioni di disequazioni o di sistemi di disequazioni.

4. Successioni e famiglie di curve

Derive rappresenta graficamente un vettore come un punto. Se vogliamo rappresentare la successione dobbiamo dunque disegnare i punti [n, ].

Possiamo per questo sfruttare la funzione vector la cui sintassi è:

vector( f(n), n, a, b, step )

(genera il vettore che consiste degli oggetti f(n) quando n varia da a a b con passo step; se step non è specificato per default è 1)

Nel nostro caso dunque f(n)= [n, ]. Semplificando tale espressione si ottengono i punti desiderati, punti che poi si possono rappresentare nella finestra grafica.

Esempi: studiare le successioni

 

Analogamente possiamo studiare famiglie di equazioni (al variare di un parametro).

Ad esempio semplificando l’espressione

vector(, d, -3, 3, 1)

si ottiene il vettore che ha per componenti le 7 parabole . Rappresentando graficamente tale vettore si ottengono in un colpo solo i 7 grafici.

Esempi:

 

5. Superfici nello spazio

Derive è molto potente per rappresentare superfici in 3D. Dopo aver inserito lequazione nella finestra algebra, passare alla finestra grafica 3D e disegnare la superficie.

Un doppio clic sul grafico consente di cambiarne il colore e il numero di pannelli (punti che derive usa per tracciare il grafico).

Si può inoltre far ruotare il grafico utilizzando i tasti direzionali oppure zoomare con i tasti page-up , page-down;in alternativa usare gli appositi pulsanti sulla barra degli strumenti.

Esempi:

    (sella)

6. Vettori, matrici ed insiemi

Derive è in grado di operare con vettori e matrici. Per inserirli nella finestra algebra usare il menu crea > vettore (matrice) oppure usare i pulsanti corrispondenti.

Operazioni tra vettori

   

 

(per il prodotto scalare si usa il punto(.), per il valore assoluto la funzione abs, per il prodotto vettoriale la funzione CROSS)

Operazioni tra matrici

 

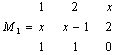
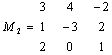
M1 +M2  M1 .M2  2M1   (M1)-1   trasp(M1)  det(M1)

(linversa di una matrice si ottiene semplificando la matrice stessa elevata alla -1, la matrice trasposta semplificando la matrice M`, semplificando la funzione det(M) si ottiene invece invece il determinante di M).

Le funzioni ROW, COL consentono invece di selezionare una o più righe (colonne) di una matrice. Consultare la guida per informazioni sull’utilizzo di tali funzioni e di altre analoghe.

Operazioni tra insiemi

Derive è anche in grado di svolgere le normali operazioni tra insiemi.

Se ad esempio

s1 = {1,2,3}   s2 = {2,3,4,5}

possiamo calcolare

      P(s2)=POWER_SET(s2)

7. Curve e superfici parametriche

Possiamo studiare curve 2D e 3D e superfici 3D parametriche, semplicemente inserendo nella finestra algebra un vettore le cui entrate dipendono da uno o due parametri.

Studiare ad esempio:

[cos t, sin(2t)],   [u cos(t),u sin(t),t]  [3sin(t),3cos(t),t]

Per curve o superfici 3D invece di tracciare il grafico usando il pulsante sulla barra degli strumenti, è meglio farlo attraverso il menu inserisci > grafico: questa procedura consente di inserire i domini dei parametri e quindi di controllare la parte di superficie che verrà visualizzata.

E facile generare superfici di rotazione attorno ai 3 assi cartesiani. Ad esempio per ottenere un toro bisogna ruotare attorno alasse z la circonferenza definita dalle equazioni parametriche:

Si ottiene

[(2+sin t) cos s,(2+sin t) sin s, cos t]

Invece ruotando la catenaria (sempre attorno all’asse z):

otteniamo il catenoide:

[cosh(t)cos(s),cosh(t)sin(s),t]

Una curva particolare è .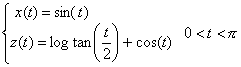

Compiendo una rotazione attorno all’asse z si ottiene la pseudosfera (curvatura di Gauss = -1):

[sin(t)cos(s),sin(t)sin(s),log(tan(t/2))+cos(t)]

Nella finestra grafica 3D il menu imposta > sistema di coordinate consente di scegliere tra coordinate cartesiane, sferiche o cilindriche.

In coordinate sferiche dobbiamo specificare nell’ordine i parametri r=raggio, s=latitudine, t=longitudine.

Esempio:

[3,s,t] rappresenta una sfera di raggio 3

la stessa cosa si può ottenere rappresentando l’espressione r=3.

In coordinate cilindriche i parametri sono invece nell’ordine s=altezza, t=angolo orizzontale, r=raggio.

Esempio:

r=3 cilindro di raggio 3

[s,t,2s] cono retto.

Il menu imposta permette di scegliere anche la regione del grafico, cioè quali punti costituiranno il cubo 3D visualizzato nella finestra grafica.

8. Derive e la geometria analitica

Problema:

In un riferimento cartesiano ortogonale, calcolare le coordinate del circocentro di un triangolo avente i vertici di coordinate A(-2;1), B(1;3), C(2,-1). Scrivere lequazione della circonferenza circoscritta.

Derive permette di risolvere un problema di questo tipo, scrivendo una serie di funzioni che costruiscono man mano i punti e le rette che ci interessano. La sintassi è la seguente:

nome_funzione(arg.1, arg.2,….):=formula_defin_funzione

P_MEDIO(P,Q):=  punto medio del segmento PQ

RETTA_ORTO(P, n) := n ? ([x, y] – P) = 0  retta ortogonale al vettore n e passante per P

ASSE(P, Q) := RETTA_ORTO(PUNTO_MEDIO(P, Q), P – Q)  asse di PQ

TRIANGOLO(P,Q,R) := [P,Q,R,P]

disegna il triangolo di vertici P,Q,R (per collegare i punti andare nel menu opzioni > visualizzazione > punti della finestra grafica e scegliere SI)

CIRCOCENTRO(P,Q,R,) := (SOLUTIONS([ASSE(P,Q), ASSE(P,R)], [x, y]))¯1

La funzione SOLUTIONS calcola un vettore di vettori delle soluzioni della forma [[xc, yc]] (1 sola soluzione).Scrivendo ¯1 derive ci restituisce la prima e in questo caso unica riga di tale matrice, cioè il punto [xc, yc].

r(P,Q,R) := ABS(P – CIRCOCENTRO(P,Q,R))  raggio della circ. circoscritta

CIRC_CIRCOSCRITTA(P,Q,R) := ABS([x, y] – CIRCOCENTRO(P,Q,R)) = r(P,Q,R)

equazione della circonferenza circoscritta

Si possono ora applicare le funzioni definite per risolvere il problema proposto.

Salvando il file in formato mth (utilità“), si salvano le funzioni così costruite, che così possono essere riutilizzate in futuro. Le utilità possono essere caricate attraverso il menu file > carica file > utilità. In questo modo derive non visualizza le funzioni sullo schermo, sebbene esse siano caricate in memoria.

Il menu dichiara > definisci funzione consente di ricordare quali funzioni sono caricate in memoria e quali argomenti utilizzano.

9. Argomenti di analisi

Derive è un valido aiuto per il calcolo di limiti, derivate e integrali. Questi strumenti si trovano tutti nel menu calcola. Si noti che lo strumento calcola > integrale apre una finestra che consente di scegliere tra integrale definito e indefinito, nel primo caso poi si scelgono gli estremi d’integrazione, nel secondo la costante di integrazione.

Esempi: Calcolo di limiti:

     

Calcolo di derivate:

   

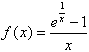
Calcolo di primitive e integrali definiti:

       

Tracciando il grafico della funzione PlotInt(u(x),x,a,b) derive visualizza l’area della regione piana compresa tra il grafico e lasse x tra x=a e x=b.

La funzione TANGENT(y, x, a) restituisce invece la retta tangente alla curva y(x) in x=a.