Zeno of Elea: the paradoxes of motion

Zeno of Elea was an ancient Greek philosopher, a disciple of Parmenides.

He is primarily known for his paradoxes—arguments that seem irrefutable yet lead to contradictory or absurd conclusions. These paradoxes were designed to support his teacher’s thesis, which argued that motion and change are illusions, and that being is unique, indivisible, and immutable.

Zeno’s Paradoxes

Zeno’s paradoxes continue to be a subject of study and debate among philosophers and mathematicians. Some of the most famous are:

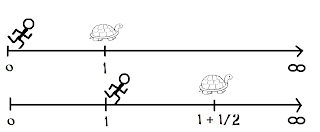
The Dichotomy: To reach point B from point A, one must first cover half the distance. However, to cover that half, one must first traverse half of it, and so on, infinitely. Thus, motion can never truly begin.

Achilles and the Tortoise: Achilles, the fastest of men, can never overtake a tortoise that has a head start. Each time Achilles reaches the point where the tortoise was, it will have moved slightly forward, and so on ad infinitum.

The Arrow: An arrow in flight is always in a specific point at each instant in time. If each instant is indivisible, the arrow is always stationary. Therefore, motion is impossible.

The Purpose of the Paradoxes

Zeno’s intent was to show, through these paradoxes, the absurdity of the idea of motion and change. He aimed to demonstrate that the only possible reality is static and immutable, as Parmenides argued.

Interpretations of the Paradoxes

Over the centuries, Zeno’s paradoxes have been interpreted in various ways:

• As a Proof of the Void: Some philosophers saw Zeno’s paradoxes as evidence for the existence of the void, necessary to explain motion.
• As a Critique of Mathematics: Others viewed the paradoxes as a critique of mathematics and the idea that the world can be described through numbers and quantities.
• As Limits of Reason: Still, others saw Zeno’s paradoxes as illustrating the limits of human reason in comprehending reality.

Zeno’s Legacy

Zeno’s paradoxes have stimulated philosophical and mathematical thought for millennia. They have helped clarify concepts of space, time, and motion and laid the groundwork for the development of logic and mathematics.

Zeno’s Influence on Medieval Philosophy

Zeno’s influence on medieval philosophy was indirect and often mediated by other authors. Nevertheless, certain Zenonian concepts left a lasting impact:

• The Problem of the Continuum: Zeno’s paradoxes intensified debates about the nature of the continuum, or the infinite divisibility of space and time—a central issue for many medieval philosophers.
• Theory of Knowledge: Some medieval thinkers used Zeno’s paradoxes to question the possibility of certain, objective knowledge of the sensible world.
• Theology: Some theologians used Zeno’s paradoxes to support the existence of God as the first cause and creator of an ordered universe.

In summary, Zeno’s paradoxes encouraged medieval philosophical and theological reflection, contributing to a deeper exploration of fundamental issues in metaphysics and epistemology.

Zeno’s Influence on Kant’s Philosophy

Immanuel Kant, one of the greatest philosophers of the modern era, extensively addressed issues of space, time, and motion—topics previously raised by Zeno.

• Nature of Space and Time: Kant argued that space and time are not properties of objects but rather a priori forms of our sensible intuition. In other words, space and time are necessary conditions for us to have any sensory experience.
• Antinomies of Pure Reason: Kant identified four antinomies, or pairs of apparently equally valid yet contradictory propositions. Some of these antinomies closely resemble Zeno’s paradoxes. For instance, the antinomy of the world in time addresses whether the world has a beginning or is infinite in the past.

How Did Zeno Influence Kant?

While a direct link between Zeno and Kant is difficult to establish, it is evident that both grappled with fundamental questions about the nature of reality, space, and time. Zeno’s paradoxes can be seen as a starting point for Kant’s reflections on human knowledge and the limits of reason.

The Relationship Between Zeno’s Paradoxes and Einstein’s Theory of Relativity

At first glance, it might seem strange to connect an ancient Greek philosopher like Zeno to a modern scientist like Einstein. However, their ideas have surprising points of intersection.

• Relativity of Motion: One of Zeno’s paradoxes, the “masses in the stadium,” anticipates the idea of the relativity of motion. Zeno describes how a moving object may appear to move at different speeds depending on the point of reference. This concept underlies Einstein’s theory of relativity, which shows that the speed of light is constant in all inertial frames of reference, and that space and time are relative and interconnected.
• Infinity and Divisibility: Zeno’s paradoxes raise questions about the nature of infinity and the divisibility of space and time. Modern physics, especially quantum mechanics, has revisited these questions, revealing a discrete structure of matter and energy at the microscopic level.

In summary, Zeno’s paradoxes, although formulated in a vastly different philosophical context, anticipate some of the fundamental questions addressed by modern physics, demonstrating the philosophical reflection’s capacity to foreshadow scientific development.

Achilles and the Tortoise in Light of Relativity Theory

The Achilles and the Tortoise paradox, seemingly distant from the complexity of relativity theory, actually hides some surprising affinities.

• The Concept of Limits: Both Zeno and Einstein prompt us to consider the nature of limits. Zeno, with his paradox, shows how dividing space and time infinitely can create the illusion that an event (Achilles overtaking the tortoise) might never happen. Einstein, on the other hand, reveals the speed of light as an insurmountable limit—a concept that challenges our classical intuition of space and time.
• Relativity of Motion: Both figures encourage us to consider that motion is always relative to a reference frame. In relativity, there is no absolute time or space; everything depends on the observer’s viewpoint. Similarly, in Zeno’s paradox, the distance Achilles must cover depends on the perspective from which we observe the race.

In summary, both Zeno and Einstein show how our intuition about space and time can be misleading, necessitating more sophisticated conceptual tools to understand reality.

The Relationship Between Zeno’s Paradoxes and Bergson’s Philosophy

Henri Bergson, a French philosopher of the 19th and 20th centuries, dedicated much of his work to reflecting on the nature of time and motion. Zeno’s paradoxes served as a source of great inspiration for him.

• Time as Duration: Bergson criticizes the notion of time as a mere succession of instants, as implied by Zeno’s paradoxes. For Bergson, time is a duration, a continuous and indivisible flow. Time is not measurable but lived.
• Intuition and Intellect: Bergson distinguishes between intuition and intellect. The intellect, he argues, tends to fragment reality into successive instants, as in the Achilles paradox. Intuition, on the other hand, allows us to grasp reality in its entirety, in its flow.

In summary, Bergson revisits Zeno’s paradoxes to criticize a conception of time too focused on measurement and quantification, and to emphasize intuition’s role in understanding reality.

The Implications of Zeno’s Paradoxes for Quantum Physics

Quantum physics, with its concepts of state superposition, entanglement, and the uncertainty principle, offers a new perspective on Zeno’s paradoxes.

• Measurement Paradox: The measurement paradox in quantum mechanics states that merely measuring a system can alter its state, somewhat recalling Achilles’ paradox. In both cases, the observation process seems to interfere with the reality we seek to measure.
• Nature of Reality: Both Zeno’s paradoxes and quantum mechanics prompt us to reconsider our understanding of reality. The quantum reality differs significantly from what our senses perceive, and Zeno’s paradoxes reveal how intuition can be misleading.

In summary, Zeno’s paradoxes, although formulated in a very different context, continue to be relevant to quantum physics. They show us that our understanding of reality is constantly evolving, and that philosophy and science are deeply intertwined.

The Arrow Paradox in Light of Quantum Mechanics

Zeno’s arrow paradox, one of his most famous, argues that an arrow in flight is always in the same point at each instant of time, and thus is, in reality, stationary. Quantum mechanics, with its subatomic-level description of reality, offers an interesting perspective on this paradox.

• Wave-Particle Duality: Quantum mechanics tells us that particles, like electrons, can behave as both waves and particles. A moving particle can be described by a wave function propagating through space. This wave function represents all possible positions the particle may occupy. Thus, in a way, the particle “exists” in all these positions simultaneously until measured.
• Wave Function Collapse: When we perform a measurement, the wave function “collapses” and the particle assumes a defined position. This means that the concept of “position” at the quantum level is more nuanced than our classical intuition.

How Does This Relate to the Arrow Paradox?

If we apply quantum mechanics to the arrow, we could say that the arrow is not a classical object with a precisely defined position at each instant. Instead, its position is described by a wave function that propagates through space, suggesting that the arrow is never “stationary” in a precise point but exists in a superposition of states, in motion.

In conclusion, quantum mechanics provides a resolution to the arrow paradox by showing that our classical intuition of space and time may be inadequate for describing reality at a microscopic level.

Modern Physics’ Insights into Zeno’s Paradoxes

The development of calculus by Newton and Leibniz resolved Zeno’s paradoxes mathematically by introducing the concept of limits, which allow an infinite series to converge to a finite result. However, the philosophical questions Zeno raised continue to echo in modern physics. His paradoxes challenge us to rethink the nature of reality, space, and time—concepts fundamental to both philosophy and physics.

Conclusion: The Enduring Relevance of Zeno’s Paradoxes

Zeno’s paradoxes are much more than intellectual puzzles; they address profound questions about the nature of reality, perception, and reason. In grappling with Zeno’s paradoxes, we encounter the limits of human understanding and confront the mysteries of the universe. Through these paradoxes, Zeno invites us to question our assumptions and expand our understanding of the world.

From mathematics to modern physics, Zeno’s paradoxes continue to inspire and challenge us, demonstrating the power of philosophical reflection to deepen our understanding of reality.